Namespace-based language modelling
David Schmidt
Kansas State University

Abstract

In the talk, the methodology is applied to a simple example to explore the choices available to a DSL designer.

1 Background

It is unlikely you will use denotational semantics or structural operational semantics to design your language. (But I must admit, I like Scott-Strachey denotational semantics!)

Why are these semantics methods little used ?

There is a huge gap between the semantics metalanguage (lambda-calculus, inference-rule sets, etc.) and the implementation (storage layout, data structures, etc.). Surely, we can do better.

1.1 Let's keep Strachey's design principles but replace the lambda calculus

A language design should include

1. the primitive (data) domains that the language (and its machine) manipulate. (Think about the domains in a DSL like MATLAB or HTML or Tcl/Tk or SQL or Perl or Ajax or ....)
2. A runtime machine model that includes the domains and clearly pictures concrete implementations. (Example: lambda-calculus modelling portrays ``lambda machines,'' which are not clear pictures of implementations.)
3. syntax that ''follows the semantics'': syntax is (merely!) notation for manipulating the machine --- for expressing the domains and the operations of the runtime model. (Tennent's extension principles add naming, parameter, and scoping constructions to the ''core syntax.'')

1.2 A starting point: The standard model for C

• The values (ints) stored in memory are the storable values.
• The values (location-ints) stored in the symbol table are the denotable values.
• The values computed by the interpreter from syntactical expressions are expressible values.

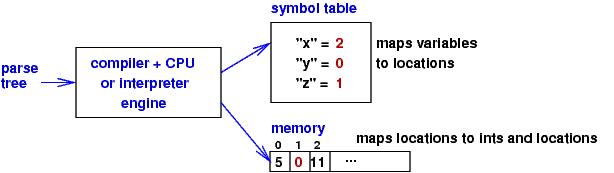
We must express in syntax the domains and operations of the runtime machine:

===================================================

C : Command                      L : LefthandSide
E : Expression                   I : Identifier
D : Declaration                  N : Numeral

C ::=  L = E | C1 ; C2 | while ( E ) { C } | if ( E ) { C1 } else { C2 }

E ::=  N  |  ( E1 + E2 )  |  L  |  & L

L ::=  I  |  * L

N ::=  string of digits
I ::=  strings of alphanumerics 

===================================================

y = 5 ;
z = &y ;      # store in  z's  cell the location named by  y
x = (6 + *z)  # add 6 to the int stored where  z  points and assign
  

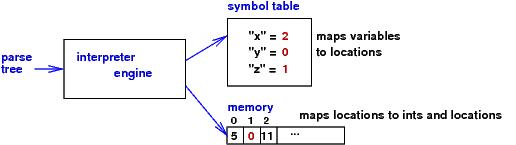
We might express in the syntax the symbol table and memory themselves. Indeed, C lets you express approximations of both --- a struct is a C-coded "baby symbol table", and an array is a C-coded "baby memory". (We won't develop them here....)

Now, we can enrich the syntax with naming devices --- declarations (or if you are Bjarne Stroustrup, lots more!).

2 Namespace-based semantic modelling

1. define the language's primitive domains and their operations

2. define the runtime model with namespaces

3. represent the model in syntax and extend the syntax by Tennent's principles.

What is a namespace?

creation:  {n1=v1, n2=v2, ... nm=vm}, for m >= 0, creates a namespace with bindings ni=vi.

membership:   n in d   returns True iff there is a binding, n=v, in d.

lock:   lock d   prohibits creation of new names in d. (Existing names can be updated, however.)

update:   d[n] = v    If n in d, replaces the existing binding for n in d by n=v. If ¬(n in d) and d is unlocked, it adds n=v to d (else erroneous).

lookup:   d[n]   returns the v such that n=v is in d. (If not(n in d), erroneous.)

let d = {'x'=2}
d['y'] = d['x'] + 1
lock d
d['x'] = 1

Namespaces appear in semantic models as

symbol tables environments hash tables

record structs objects activation records

They can also model closures, stacks, finite-domain functions, vectors....

2.1 A runtime model designed with namespaces

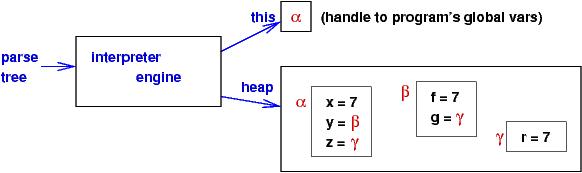
There is a distinguished handle, named this, which is the handle to the "active namespace" whose bindings are visible to the interpreter while it interprets commands.

===================================================

C : Command                 L : LefthandSide
E : Expression              I : Variable
F : FieldName               N : Numeral

C ::=  L = E  |  if E : C1 else C2  |  while E : C  |  C1 ; C2

E ::=  N  |  ( E1 + E2 )  |  L  |  new { F }

F ::=  I  |  I , F

L ::=  I  |  L . I  |  this

N ::=  string of digits
I ::=  strings of letters, not including keywords

===================================================

x = 7; y = new {f, g}; y.f = x; y.g = new {r}; z = y.g; z.r = y.f;

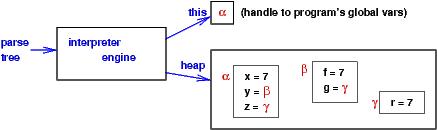
The syntax for new namespaces (new{I1,I2,...}) is inadequate; here is one that lets us initialize the new namespace:

E ::=  . . .  |  new { C }

x = 7;
y = new { f = super.x;
          g = new {}     // (*)
        };
z = y.g;
z.r = y.f

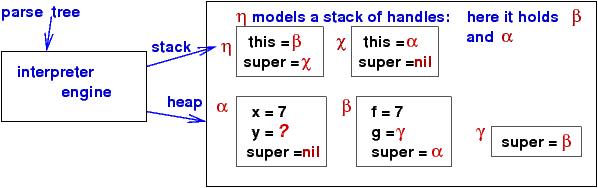
To implement new{C}, there must be a stack (or list) of handles (an activation stack) of the active namespaces. In the diagram, the stack is a linked list of dictionaries with fields this (the "top"/"head") and super (the "rest"/"tail"). The semantics of new{C} goes:

(i) allocate a new namespace and push its handle on the stack;

(ii) evaluate C, using the top handle (η['this']) as the active namespace;

(iii) pop the stack;

(iv) lock the new namespace and return its handle.

Our proposed new{C} generates scoping conflicts, e.g.,

x = 7;
y = new {z = x; x = 0}

var x = 7;
var y = new {var z = x; x = 0}

var x = 7;
var y = new {var z = x; var x = 0}

this.x = 7;                      
this.y = new {this.z = x; x = 0}

Again, var I = E means to bind I to E's value in the active namespace. In contrast, I = E locates the L-value for an already existing I along the chain of super links (the "static chain") and updates I at the nearest namespace where I already exists.

We are a short step from functions, classes, and methods --- we will apply Tennent's naming conventions to derive these from the core syntax. This is coming.

2.2 Semantics definition == Prototype interpreter

===================================================

P : Program
C : Command           E : Expression
T : Template          L : Lefthandside

P ::=  T

C ::=  var I = E  |  L = E  |  C1 ; C2  |  while E : C end

E ::=  N  |  ( E1 + E2 )  |  L  |  new T

T ::=  { C }

L ::=  I  |  L . I  |  this  |  super

===================================================

===================================================

Storage structure:
  heap : Dictionary of { Handle :  Namespace }
           // has an operation,  allocateNS(d), where the bindings in  d
           //   are copied into a newly allocated namespace in  heap  and
           //   the handle to the new namespace is returned 
  actstack : Handle
           // is the handle to the front of a linked list of  {'this', 'super'}
           // cells in the heap (the dynamic chain of activation records).
           // There are the expected  push, pop, top  operations.
  where  Namespace = Dictionary of { Identifier : Denotable }
         Denotable = Handle | Int
         LValue = (Handle , Identifier)
  and Handle is the set of namespace addresses  and  Int is the set of integers


Program[[.]] updates heap:

[[ T ]] = Template[[ T ]]


Command[[.]] updates heap:

[[ var I = E ]] ==  heap[top()][I] = Expression[[ E ]]

[[ L = E ]] ==  let (han,id) = Lefthandside[[ L ]]
                heap[han][id] = Expression[[ E ]]

[[ while E : C end ]] ==  while Expression[[ E ]] != 0 :
                            Command[[ C ]]

[[ C1 ; C2 ]] == Command[[ C1 ]]
                 Command[[ C2 ]]


Expression[[.]] updates heap and returns Denotable:

[[ N ]] == return int(N)

[[ E1 + E2 ]] == let n1 = Expression[[ E1 ]]
                 let n2 = Expression[[ E2 ]]
                 return add(n1, n2)

[[ L ]] == let (han,id) = Lefthandside[[ L ]] 
           return heap[han][id]

[[ new T ]] == let han = Template[[ T ]]
               lock han
               return han


Template[[.]] updates heap and returns Handle:

[[ { C } ]] == let newhandle = allocateNS({'super' = top()})
               push(newhandle)
               Command[[ C ]]
               pop()
               return newhandle


Lefthandside[[.]] returns LValue:

[[ I ]] == let han = top()
           let found = False 
           // find the most local instance of  I  in the static chain:
           while not found and han != nil :  
               if I in heap[han] : found = True
               else : han = heap[han]['super']
           return (han, I)

[[ L . I ]] == let (han,id) = Lefthandside[[ L ]]
               let han2 = heap[han][id]
               return (han2, I)

[[ this ]] == return (actstack, 'this') 

[[ super ]] == return (top(), 'super')

===================================================

Comments:

• The semantics defines a meaning for every syntactically well-formed, non-erroneous program. a program that that is erroneous (e.g., var x = this + 2) has no meaning.

• The language lets the programmer construct namespaces --- ''little heaps'' --- via new{...}, so we are moving towards an object language. (If we want to model C, we start with vectors, not namespaces.)

• There are two forms of indexing (of Lefthandside forms): I is an internal indexing starting from the active scope (namespace), progressing along the static chain of super links, and L.I is an explicit, external indexing from one scope into another. The two lookup methods prove critical later when we distinguish between ``private'' and ''public'' fields.

• The semantics of a program, P, is Template[[ P ]], conducted with heap = {} and actstack = nil. That is, a program constructs the main namespace in the heap.

• The semantics of new{C} always locks its newly allocated namespace. We can relax this requirement with these small adjustments:

  We add an explicit lock operation to the syntax:

  E ::=  . . . |  new T  |  ! E
  

  Here are the revised semantics:

  Expression[[ new T ]] == return Template[[ T ]]
  
  Expression[[ ! E ]] == let han = Expression[[ E ]]
                         lock han
                         return han
  

  With the variant, we can lock a namespace whenever we wish:

  var ob = new { var f = !new {var x = 0} }; 
  ob.g = ob.f.x;
  ob = !ob  
  

• The language's semantics lets a program alter its own scope, e.g,

  var ob = new { var f = 1 };
  this = ob;
  f = 2;
  this = super
  

  If desired, we can disallow such activity by restricting the syntax of Lefthandsides:

  L ::=  I  |  this . I  |  super . I  |  L . I
  

3 Tennent's naming principles

===================================================

C ::=  var I = E  |  L = E  |  C1 ; C2 

E ::=  N  |  ( E1 + E2 )  |  L  |  new T

T ::=  { C }

L ::=  I  |  L . I  |  this

===================================================

• Abstraction principle: Phrases of a syntax class can be named (declared); the named phrases are called abstracts.
• Parameterization principle: An abstract may be annotated by parameters, which bind to arguments from a syntax class.
• Qualification principle: The phrases of a syntax class may own private declarations.

3.1 Abstraction principle

===================================================

C : Command            D : Declaration
T : Template           E : Expression
L : Lefthandside       N : Numeral       I : Variable

D ::=  proc I : C  |  class I : T  |  var I = E

C ::=  L = E  |  C1 ; C2  |  D  |  L ( )

E ::=  N  |  ( E1 + E2 )  |  L  |  new T

T ::=  { C }  |  L ( )

L ::=  I  |  L . I  |  this

===================================================

var I = {'code' = 'C}  // where  'super'  holds  C's  static link to its globals

class clock : { var time = 0;
                proc tick : time = time + 1 end};

var j = new clock();
var k = new clock();
k.tick()

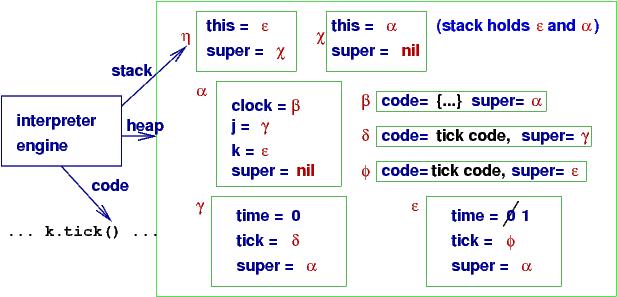
IMPORTANT: No new computational machinery is added to the model. This is the beauty in Tennent's approach --- it exploits the computational abilities already in place.

Perhaps you are thinking, ``where is the activation record for tick's call?'' We'll examine this shortly....

Here is the semantics; it is essentially identical for both classes and procedures, but we repeat it to emphasize exactly that point:

===================================================

Declaration[[ proc I : C ]] == let active = top()
                               let han = allocateNS({'code' = C, 'super' = active})
                               lock(han)
                               heap[active][ I ] = han

Command[[ L() ]] == let (han,id) = Lefthandside[[ L ]]
                    let closure = heap[ heap[han][id] ]
                    push(closure['super'])
                    Command[[ closure['code'] ]]
                    pop()

Declaration[[ class I : T ]] == let active = top()
                                let han = allocateNS({'code' = T, 'super' = active})
                                lock(han)
                                heap[active][ I ] = han

Template[[ L() ]] == let (han,id) = Lefthandside[[ L ]]
                     let closure = heap[ heap[han][id] ]
                     push(closure['super'])
                     let newhan = Template[[ closure['code'] ]]
                     pop()
                     return newhan

===================================================

3.2 Parameterization principle

var time = 0;
proc tock(): 
   var m = 2;
   time = time + m
end;

In any case, the question is moot once we allow parameters to procedures --- for each call, we must allocate an activation record (namespace) to hold the parameter-arguments bindings. For this syntax,

===================================================

D ::=  proc I1 ( I2 ) : C  |  class I1 ( I2 ) : T
C ::=  . . .  |  L ( E )
T ::=  . . .  |  L ( E )

===================================================

class clock(init, increment): { var time = init;
                                proc tick():
                                    time = time + increment;
                                proc reset(what):
                                    var w = what + increment;
                                    time = w }
var j = new clock(3, 1);
j.reset(0)

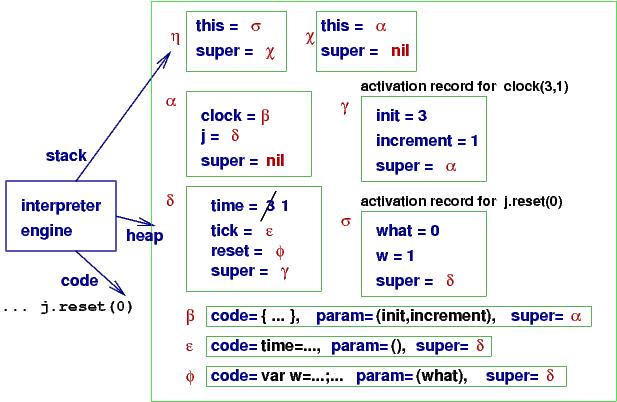
The semantics definition shows that an activation record is allocated when the procedure is called with its argument:

===================================================

Declaration[[ proc I1 ( I2 ) : C ]] == let active = top()
                                       let han = allocateNS(
                                            {'param'= I2, 'code'= C,
                                             'super'= active} )
                                       lock(han)
                                       heap[active][ I1 ] = han

Command[[ L ( E ) ]] == let (han,id) = Lefthandside[[ L ]]
                        let closure = heap[ heap[han][id] ]
                        let arg = Expression[[ E ]]
                        let han2 = allocateNS({'super' = closure['super'],
                                               closure['param'] = arg})
                        push(han2)
                        Command[[ closure['code'] ]]
                        pop()

===================================================

3.3 Qualification principle

begin D in C end

For commands, the semantics looks like this:

Command[[ begin D in C end ]] == let han = allocateNS({'super' = top()})
                                 push(han)
                                 Declaration[[ D ]]
                                 lock han
                                 Command[[ C ]]
                                 pop()

On the other hand, the format works well for templates:

===================================================

T ::=  { C }  |  private D in T  |  L ( E )

Template[[ private D in T ]] == let han = allocateNS({'super' = top()})
                                push(han)
                                Declaration[[ D ]]
                                lock han
                                let han2 = Template[[ T ]]
                                pop()
                                return han2

===================================================

Other phrase forms can use blocks, but modern languages often marry blocks to parameterized abstracts, so that the private declarations are treated like extra parameter bindings. This approach works fine for straightforward examples, like this one:

class clock(init, increment) private  var time = init :
    { proc tick(): time = time + increment end;
      proc reset(what): time = what end
    }

var c = new  private var init = 0; var increment = 2; var time = init
             in { proc tick(): time = time + increment end;
                  proc reset(what): time = what end
             }

It is easy to modify the semantics of parameterized abstracts to store private declarations: For the format, class I1 (I2) private D : T, the semantics of the class declaration is to store within a closure all of I2, D, and T. The semantics of the class's call, L(E), is to locate the closure named by L's L-value, allocate a new namespace, insert into it I2 bound to E's value, push the namespace, evaluate D (its bindings will be deposited into the new namespace), and then evaluate T. At conclusion, the namespace is popped.

Public and private fields

D ::=  private var I = E  |  private proc I1 ( I2 ) : C end  | ...

===================================================

Declaration[[ private var I = E ]] ==  heap[top()][I] = Expression[[ E ]]
                                       markPrivate(top(), I)

Declaration[[ private proc I1 ( I2 ) : C ]] == let active = top()
                                               let han = allocateNS(
                                                 {'param'= I2, 'code'= C,
                                                  'super'= active} )
                                               lock(han)
                                               heap[active][ I1 ] = han
                                               markPrivate(active, I1)

===================================================

External (dot) indexing cannot locate a private L-value:

===================================================

Lefthandside[[ L . I ]] == let (han,id) = Lefthandside[[ L ]]
                           let han2 = heap[han][id]
                           if  not isPrivate(han2, I): return (han2, I)
                           else : return (nil, I)

===================================================

(NOTE: Object languages that use public and private labels on object fields almost always check their uses with a compiler so that the the labels are not embedded with the fields in the run-time objects --- label checking is part of the compiler's "type checking". This section exists so to emphasize that dot indexing can never be used to reference a private field.)

3.4 Objects as compound namespaces and the semantics of this

Recall that the pronoun, this, denotes the active namespace, which to this point coincided with the notion of ``this object.'' Now that objects are compound namespaces, the correspondence breaks down, and we must alter the semantics of this to denote ``this object,'' a concept that differs from ''this namespace.'' Here is a simple use of this in a object-oriented language:

class C() : { var f = 0;
              proc p(f) : this.f = f  end };
var ob = new C();
ob.p(3)

Why does this happen? A typical object-oriented language decodes the call, ob.p(3) like this:

1. Evaluate ob.p to the L-value, (α, p).
2. Create a new activation (namespace) for the call to p, and save in it these bindings: f = 3, this = α. The name, this, is treated as an extra parameter name.
3. The assignment, this.f = f, computes as expected, because this.f computes the L-value, (α,f), and f computes to a lookup of the parameter f, which yields 3.

a call, objectName.methodName(args), computes the handle for objectName, which is bound to the name, this, for the execution of the body of methodName.

There is a simple semantics that explains the above steps. To employ it, we make one significant restriction to the programming language:

• It is now illegal for the handle of a closure object to be an expressible value (that is, the value of an expression). That is, we will disallow this kind of free-wheeling use of closures:

  var c = new { var x = 1;
                proc p(y): this.x = y  end
              };
  var d = new { var x = 2;
                var f = c.p   // c.p  alone cannot be a legal expression
              };
  
  d.f(99)
  

  Procedure p means to update the x in c, but d.f(99) suggests an update of x in d. (Should this bind to c's handle or to d's handle?) We avoid the confusion by prohibiting c.p as an expressible value.

  (IMPORTANT: we can remove the restriction if we add a new form of closure, a partially evaluated call, to the machine model. Such a closure holds a procedure's code, its parameter names, some (not all!) of the arguments that bind to the parameter names, and a super-link. We won't use this closure here, but it is indeed doable and plays a significant role in implementations for Python and OCAML.)

Here are the revisions in the semantics of expressions, lefthandsides, and procedure call:

===================================================

Expression[[ L ]] ==  let (han, id) = Lefthandside[[ L ]]
                      let val = heap[han][id]
                      if notHandleToClosure(val) : return val
                      (else erroneous)

Command[[ L ( E ) ]] ==  let (han,id) = Lefthandside[[ L ]]
                         let closure = heap[ heap[han][id] ]
                         let arg = Expression[[ E ]]
                         let han2 = allocateNS({'super' = closure['super'],
                                                closure['param'] = arg,
                                                'this' = han  })
                         push(han2)
                         Command[[ closure['code'] ]]
                         pop()

Lefthandside[[ I ]] == ...as before...

Lefthandside[[ L . I ]] == ...as before...

Lefthandside[[ this ]] == if 'this' in heap[top()] :
                             return (top(), 'this')
                          else : return (actstack, 'this')



===================================================

The treatment of this as an extra procedure parameter is required for defining subclasses and method override, which come next.

3.5 Subclasses

Tennent's extension principles do not yield subclasses. Indeed, subclassing is an operation on templates, independent from abstracts, parameters, and blocks. In its most general form, it is a ``template append'' operation:

T ::=  { C }  |  L ( E )  |  T1 + T2

class Point(a,b) : { var x = a;  var y = b;
                     proc paint() : ...x...y...a...b... end;
                     proc display() : this.paint() end
                   };
class Color(c) : { var color = c;
                   proc paint(...) : super.paint(); ...color... end
                 };

class ColoredPoint(x,y,c) : Point(x,y) + Color(c);
var RGB = 999999;
var p = ColoredPoint(0,0,RGB)

===================================================

D ::=  ...  |  class I1 ( I2 ) : T  |  var I = E

E ::=  ...  |  new T

T ::=  { C }  |  L ( E )  |  extends T with { C } 

L ::=  this  |  super  |  I  |  L . I

===================================================

class Point(a,b) : { var x = a;  var y = b;
                     proc paint() : ...x...y...a...b... end;
                     proc display() : this.paint() end
                   };
class ColoredPoint(m,n,c) : extends Point(m,n) with
                 { var color = c;
                   proc paint(...) : super.paint(); ...color... end
                 };

var p1 = new Point(0,0);
var p2 = new ColoredPoint(9,88,777)

And there is the notion of ``superobject'' (``superclass''), as used in super.paint() --- p2's paint method will call the paint method in the ``superobject part'' of p2.

Finally, there is virtual-method override at work: the call, p2.display(), invokes the method display in Point, whose call, this.paint(), activates the paint method in ColoredPoint (whereas, p1.display() activates paint in Point).

All these issues will be handled by a new linkage, implemented by a new field, 'superob', which links subclass-namespaces to superclass-namespaces.

The semantics is revised so that an object becomes a sequence of namespaces linked together by 'superob' links. To implement correctly this and virtual-method lookup, we restrict the semantics so that

The only handles that are expressible values are those handles that are returned by the new T construction.

In the above example, p2.display will compute to a well-defined L-value, of the form, (handleOf_p2, 'display'). But display is not stored within the namespace named by handleOf_p2. We must adjust the semantics of dereferencing to locate the closure for display in the super-namespace of the compound object named by the handleOf_p2.

We do this with a search along the chain of 'superob' links --- this is virtual-method lookup.

Here is the syntax of the relevant fragment of the language, including a some phrases whose semantics remain the same:

===================================================

D ::=  proc I1 ( I2 ) : C  |  class I1 ( I2 ) : T  |  var I = E

C ::=  L = E  |  D  |  L ( E )

E ::=  L  |  new T  |  ! E

T ::=  { C }  |  L ( E )  |  extends T with { C }  |  private D in T

L ::=  this  |  I  |  L . I  |  super . I

===================================================

===================================================

virtualLookup((han, id), linkname) ==
           // starting from handle  han,  searches for  id  in the namespaces 
           // along the linkage indicated by  linkname  and
           // returns the exact L-value where  id  resides
           let h = han
           let found = False
           while not found and h != nil :
               if I in heap[h] : found = True
               else : h = heap[h][linkname]
           return (h, I)


Declaration[[.]] updates heap

[[ proc I1 ( I2 ) : C ]] == let active = top()
                            let han = allocateNS( {'param'= I2, 'code'= C,
                                                   'super'= active} )
                            lock(han)
                            heap[active][ I1 ] = han

[[ class I1 ( I2 ) : T ]] == let active = top()
                             let han = allocateNS( {'param'= I2, 'code'= T,
                                                   'super'= active} )
                             lock(han)
                             heap[active][ I1 ] = han 

[[ var I = E ]] ==  heap[top()][I] = Expression[[ E ]]


Command[[.]] updates heap:

[[ D ]] ==  Declaration[[ D ]]

[[ L = E ]] ==  let (han, id) = virtualLookup(Lefthandside[[ L ]], 'superob')
                heap[han][id] = Expression[[ E ]]

[[ L ( E ) ]] == let (object_handle, id) = Lefthandside[[ L ]]
                 let (han,id) = virtualLookup((object_handle, id), 'superob')
                 let closure = heap[ heap[han][id] ]
                 let arg = Expression[[ E ]]
                 let han2 = allocateNS({'super' = closure['super'],
                                        closure['param'] = arg,
                                        'this' = object_handle })
                 push(han2)
                 Command[[ closure['code'] ]]
                 pop()


Expression[[.]] updates heap returns Denotable:

[[ L ]] ==  let (han,id) = virtualLookup(Lefthandside[[ L ]], 'superob')
            let val = heap[han][id]
            if notHandleToClosure(val) : return val  (else erroneous)

[[ new T ]] ==  return Template[[ T ]]

[[ ! E ]] ==  lock Expression[[ E ]]


Template[[.]] updates heap and returns Handle:

[[ { C } ]] == let newhandle = allocateNS({'super' = top(),
                                           'superob' = nil})
               push(newhandle)
               Command[[ C ]]
               pop()
               return newhandle

[[ extends T with { C } ]] == let han1 = Template[[ T ]]
                              let han2 = allocateNS({'super' = top(),
                                                     'superob' = han1})
                              push(han2)
                              Command[[ C ]]
                              pop()
                              return han2

[[ private D in T ]] == let han = allocateNS({'super' = top()})
                        push(han)
                        Declaration[[ D ]]
                        lock han
                        let han2 = Template[[ T ]]
                        pop()
                        // make  T's  object own  D's  decls:
                        heap[han]['this'] = han2
                        return han2

[[ L ( E ) ]] == let (han,id) = virtualLookup(Lefthandside[[ L ]], 'superob')
                 let closure = heap[ heap[han][id] ]
                 let arg = Expression[[ E ]]
                 let han = allocateNS({'super' = closure['super'],
                                       closure['param'] = arg})
                 push(han)
                 let han2 = Template[[ closure['code'] ]]
                 pop()
                 return han2


Lefthandside[[.]] returns LValue:
//  the LValue has form, (object_handle, field), where  object_handle 
//  is the entry handle into the compound namespace where  field  is located

[[ I ]] ==  virtualLookup((top(), I), 'super') 

[[ L . I ]] == let (han,id) = virtualLookup(Lefthandside[[ L ]], 'superob')
               let han2 = heap[han][id]
               return (han2, I)

[[ this ]] ==  if 'this' in heap[top()] :
                   return (top(), 'this')
               else :
                   return (actstack, 'this')

[[ super . I ]] ==  if 'this' in heap[top()] :
                         han = heap[top()]['this']['superob']
                    else : han = heap[top()]['superob']
                    return (han, I)

===================================================

4 Modelling Domain-Specific programming Languages

A DSL uses concepts familiar to people who work in a specialized problem domain. For example, say that you must install an alarm system in an office building. A DSL for sensor-alarm networks would discuss

• domains: sites (building, floor, hallway, room), devices (alarm, movement detector, camera, badge), people (employee, guard, police, intruder). These are the ``nouns'' of the DSL.
• Domain elements have features/attributes (``adjectives'') and operations (''verbs'').
• Actions (``sentences'') are initiated by events.

``when a movement detector detects an intruder in a room, it generates a movement-event for a camera and sends a message to a guard....''

''It would be nice to have a little language to help me do ...this job....''

4.1 Top-down DSL

A top-down DSL has a mix of assets and drawbacks:

+ non-programmers can discuss and use the DSL

+ the DSL encourages standard patterns of design and implementation

+ there is fast development of programs that fall in the problem domain

- staff must be trained to use the DSL

- the interaction of DSL-generated software with other software components can be difficult

- there is a high cost in designing, developing, and maintaining a DSL

4.2 Bottom-up DSL

A bottom-up DSL ``extends'' a general-purpose language, the host language, with a library of data structures and operations specific to the problem domain. GUI-building languages are bottom-up DSLs, e.g., Swing (in Java), Tkinter (in Python), and Glade (in C).

Experienced programmers naturally become bottom-up DSL designers, because they develop libraries they use repeatedly. Eventually, their programs consist mostly of their library components and a little ``glue code'':

The programmer has extended the host language ``upwards'' towards the problems to be solved.

A bottom-up DSL has its strengths and weaknesses also:

+ It integrates well with applications written in its host language

+ Its development and maintenance is managed naturally over the time period when it is used, since it is an ``organic,'' library that adapts to its applications.

- Its range of users is largely limited to experienced programmers, perhaps just to the people who develop and maintain the library.

- Its ease of use is connected to the ease of use of the underlying host language.

4.3 Applying semantic models to DSL design

• Top down:
  1. select application domains;
  2. design runtime model;
  3. design syntax to manipulate the model;
  4. write semantics/protoype.

  The runtime model you design must be natural and understandable to the domain's users. In particular, choose carefully the language's command/control structures. (E.g., physicists might not enjoy writing while-loops --- recurrence equations would be better.)

• Bottom up:
  1. write library components that implement the application domains;
  2. select a minimal host-language subset for writing ``glue code'' (control code);
  3. design a runtime model that matches the glue-code syntax and treats the library components as primitives. (``The semantics model follows from the syntax!'')

  Refine the libraries, model, and glue code until the library becomes ``more important'' to problem solving than the host language itself.

5 Conclusions

Our grasp of language principles depends critically on the methods we use to define the language.

Simple modelling principles that define prototype implementations work best.

Strachey's and Tennent's techniques are worth retaining; they work across a range of design methodologies.

We must make a conscious effort to use these techniques, else they will be lost to our students and successors.

6 References

Tennent, R.D. Principles of Programming Languages. Prentice-Hall, 1981.