Have you taken a Geometry class? If so, you computed the
classical way.
A tiny example: deduction laws for "less-than":
===================================================
E1 > E2 E1 > E2 E2 > E3
(add):------------------ (transitivity): -----------------------
E1 + N > E2 + N E1 > E3
===================================================
Two proofs using these laws:
===================================================
PROVE: |- x + 2 > x PROVE: a > 0, a > b |- a + a > b
1. 2 > 0 arithmetic fact 1. a > 0 hypothesis
2. x + 2 > x + 0 add 1 2. a > b hypothesis
3. x + 2 > x arithmetic on 2 3. a + a > a + 0 add 1
4. a + 0 > b + 0 add 2
5. a + a > b + 0 transitivity 3,4
6. a + a > b arithmetic on 5
===================================================
|
David Hilbert was perhaps the most influential mathematician
of the 19th (and 20th!) centuries. Hilbert believed strongly in the
computing approach to mathematics, like above, and in the 1920's he
employed many mathematicians to realize "Hilbert's program":
all true facts of mathematics can be computed by proofs using deduction laws for classical logic ("and", "or", "not", "all", "exists") and numbers (like the two laws above). This implies that all of mathematics can be done (by machines!) that mechanically apply deduction laws in all possible combinations until all true facts are computed as answers. Will this work out? Are humans unnecessary to mathematics? |
|
In 1931, a German PhD student, Kurt Gödel ("Goedel"), showed that Hilbert's program
was impossible --- he showed that mathematics was unsolvable ---
there are true facts in math that cannot be computed mechanically.
In the process, Gödel invented the modern notions of machine coding, stored program, recursive computation, and program analyzer (a program that consumes other programs as inputs). |
Greatly simplified, here's what Gödel did:
He wrote programs (logic formulas) that (i) check if a number decodes into a formula; (ii) check is a number decodes into a proof; (iii) check if a numbered proof proves a numbered formula.
He explained how to generate mechanically all combinations of all deduction laws to prove all the facts of mathematics that can be proved.
Gödel studied the deduction laws for schoolboy (Peano) arithmetic: the nonnegative ints with +, *, >, =, and he proved there are true facts of arithmetic that can never be proved by deduction laws! Gödel did this by finding a formula, which has integer number, #G, such that:
(More precisely stated, ``Formula #G cannot be proved'' is this logic formula: ¬(∃ P (decodesIntoProof(P) ∧ decodesIntoFormula(#G) ∧ proves(P, #G))), that is, ``There does not exist an int, P, that decodes into a proof of the formula numbered by int G.'')
Assume that the deduction laws (i) build proofs of only true formulas (the laws are sound) and (ii) can build proofs for all the true formulas of arithmetic (the laws are complete). Can the deduction laws for arithmetic be both sound and complete? Assume they are.
Formula #G is a logical bomb that blows up our assumption:
Side comment: It's not odd that logic formulas can code computation --- this has been known for centuries. Gödel was the first to make a computer language out of logic, and these days, the PROLOG ("PROgramming in LOGic") programming language is the preferred language for artificial intelligence, knowledge discovery, and even some data-base applications.
|
Turing was an English mathematician, employed by the British government to break the codes the Nazi armies used for communication. Turing and his team succeeded, and the Allies used the decoded Nazi communications to win World War II.
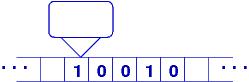
Turing was interested in mathematical games, and he was interested in the machine codings of Gödel. He conceived a machine for working with the codes. His Turing machine was a controller with a read-write head that traversed the squares of an unbounded roll of toilet paper, where only a 0
or a 1 can be written in a square:
|
move Left/Right one square erase the square (make it blank) write 0/1 on the square if square is blank/0/1, then goto Instruction #n goto Instruction #n stopHere is a sample program that scans a binary number from left to right and flips all 0s to 1s and all 1s to 0s:
#1: if square is 0, then goto #4
#2: if square is 1, then goto #6
#3: if square is blank, then goto #9
#4: write 1
#5: goto #7
#6: write 0
#7: move Right
#8: goto #1
#9: stop
... => ... 
These instructions are given number codings, so that a program written in the
instructions could be copied on a tape and read by a controller.
The Universal Turing Machine was configured like this:
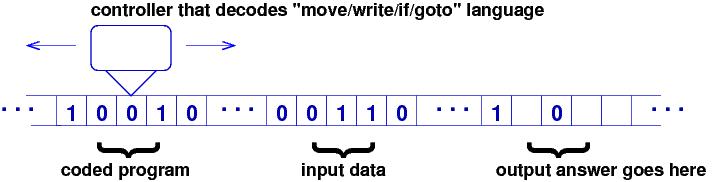
Gödel's machine codings were used to represent a program as a long sequence of 0s and 1s. The Universal Turing Machine is the origin of
Turing wrote programs for the Universal Turing machine, and all the programs of Gödel's primitive-recursive-function language were coded for the Turing machine. Turing believed that all facts/knowledge/problems that can be calculated/deduced/solved by a machine can be done by a Universal Turing Machine. This is now known as the Church-Turing thesis.
(The "Church" part refers to Alonzo Church, a Princeton mathematician who developed a symbol system, the lambda-calculus, which has the same computational powers as Turing's machines.)
Turing asked: are there some problems whose solutions cannot be calculated by his machine? Here is the problem he considered: It is the first example of a program analyzer: Is there a program that can read the machine coding of any other program and correctly predict whether the latter will loop when it runs?
This is called the halting problem.
Turing showed that the answer is NO --- there is no such program. Here's why:
H(#P) = print 0, if program #P loops when it runs
print 1, if program #P halts when it runs
(If Program #P itself needs input data, the input data number is appended on the tape to the end of int #P.)
E(#P) = start program #H with #P on the same tape as input.
Wait for the answer.
If the answer's 1, then LOOP!
If the answer's 0, then print 0
The first electronic computers were "non universal" machines, where the computer program was wired into the CPU. The wires were moved around when a new program was desired. The ENIAC people implemented Gödel's and Turing's machine language, stored programs, and "universal" CPUs.
Your computers and electronic gadgets are the offspring of Gödel's and Turing's thoughts.
The developments described here crystallized as computability theory.
First, think of a problem as a math function: you give an input argument to the function, and the function tells you an answer (output). The function defines what you must solve/implement. Now, which math functions can be mechanically computed by programs? Here are two famous groups that can:
These questions are studied within computational complexity theory. Their answers define subclasses of the μ-recursive functions. We learn about this topic by studying some simple algorithms that work with arrays.
Step 1: V
[6, 10, 2, 4, 12, 16, 8, 14]
Step 2: V
[6, 10, 2, 4, 12, 16, 8, 14]
...
Step 7: V
[6, 10, 2, 4, 12, 16, 8, 14]
We search the array from front to back. How fast is this algorithm?
Without worrying about speeds of chips, we measure the speed of an
array algorithm by how many array lookups/updates it must do.
Obviously, with an array of length 8, at most 8 lookups is needed; in general, if the array has length N, at most N lookups is needed. This is the worst-cast time complexity, and in this case is linearly proportional to the length of the array. We say that sequential search is a linear-time algorithm, order-N.
Here is a table of how a linear-time algorithm performs:
===================================================
array size, N worst-case time complexity, in terms of lookups
----------------------------------------------
64 64
512 512
10,000 10,000
===================================================
A linear-time algorithm looks "slow" to its user but is tolerable if
the data structure is not "too large".
When you write a one-loop program that counts through the elements of an array, your algorithm runs in linear time.
Find 8 in [2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22]:
Step 1: look in middle: V
[2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22]
Step 2: look in middle of left half: V
[2, 4, 6, 8, 10 ... ]
Step 3: look in middle of left's right subhalf: V
[ ..., 8, 10, ... ]
The subarray searched shrinks by half each time there is a
lookup, and the key is quickly found --- in worst case,
at most log2N lookups are needed to find the key. (Recall that
log2N = M means that 2M = N.)
This is log-time, order log-N.
Here's a table:
=================================================== array size, N linear-time log-time ---------------------------------------------- 64 64 6 512 512 8 10,000 10,000 12 ===================================================The speed-up is spectacular; this algorithm is markedly faster in theory and in practice. In practice, regardless of how a database is configured, the search operation must be order log-time or faster.
When you write an algorithm that "discards" half of a data structure during each processing step, you are writing a log-time algorithm.
Input array Output array --------------------------- -------------------- [6, 10, 2, 4, 12, 16, 8, 14] [] [6, 10, 4, 12, 16, 8, 14] [2] [6, 10, 12, 16, 8, 14] [2, 4] [10, 12, 16, 8, 14] [2, 4, 6] . . . [16] [2, 4, 6, 8, 10, 12, 14] [] [2, 4, 6, 8, 10, 12, 14, 16]The algorithm scans the N-element array N-1 times, and 1/2(N2 - N) lookups are done; there are also N updates to the output array. This is a quadratic-time algorithm, order N2. Here is the comparison table:
=================================================== array size, N linear log2N N2 1/2(N2 + N) ------------------------------------------------------- 64 64 6 4096 2064 512 512 8 262,144 131,200 10,000 10,000 12 100,000,000 50,002,500 ===================================================(Note there isn't a gross difference between the numbers in the last two columns. That's why selection sort is called a quadratic-time algorithm.)
A quadratic-time algorithm runs slowly for even small data structures. It cannot be used for any interactive system --- you run this kind of algorithm while you go to lunch. When you write a loop-in-a-loop to process an array, you are writing a quadratic algorithm.
The standard sorting algorithms are quadratic-time, but there is a clever
version of sorting, called "quicksort", that is based on a
divide-and-conquer strategy, using a kind of binary search to replace one
of the nested loops in the standard sorting algorithms. Quicksort runs in order N * log2N time:
N log2N N2 N*log2N
-------------------------------------------------------
64 6 4096 384
512 8 262,144 4096
10,000 12 100,000,000 120,000
===================================================
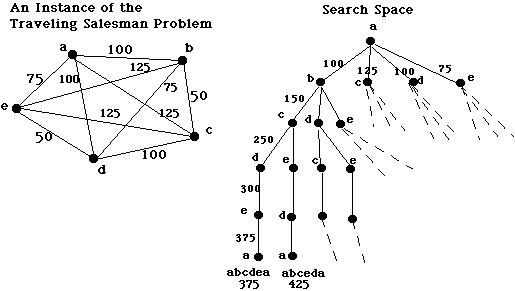
These problems require that you calculate all possible permutations (internal combinations) of a data structure before you select the best permutation. Many important industrial and scientific problems, which ask for optimal solutions to complex constraints, are minor variations of the search-problems stated here.
The problems stated above are solvable --- indeed,
here is a Python function that calculates all the permutations (shuffles) of a deck of
size-many cards:
===================================================
def permutations(size) :
"""computes a list of all permutations of [1,2,..upto..,size]
param: size, a nonnegative int
returns: answer, a list of all the permutations defined above
"""
assert size >= 0
if size == 0 :
answer = [[]] # there is only the "empty permutation" of a size-0 deck
else :
sublist = permutations(size - 1) # compute perms of [1,..upto..,size-1]
answer = [] # build the answer for size-many cards in a deck
for perm in sublist:
# insert size in all possible positions of each perm:
for i in range(len(perm)+1) :
answer.append( perm[:i] + [size] + perm[i:] )
return answer
===================================================
It uses a recursion and a nested loop. For example,
permutations(3) computes
[[3, 2, 1], [2, 3, 1], [2, 1, 3], [3, 1, 2], [1, 3, 2], [1, 2, 3]].
Try this function on your computer and see how large an argument you
can supply until the computer refuses to respond.
The solution to the above is written in just a few lines of Prolog, which is
an ideal language for calculating all combinations that satisfy a set
of constraints:
===================================================
/* permutation(Xs, Zs) holds true if list Zs is a reordering of list Xs */
permutation([], []).
permutation(Xs, [Z|Zs]) :- select(Z, Xs, Ys), permutation(Ys, Zs).
/* select(X, HasAnX, HasOneLessX) "extracts" X from HasAnX, giving HasOneLessX */
select(X, [X|Rest], Rest).
select(X, [Y|Ys], [Y|Zs]) :- select(X, Ys, Zs).
/* This query computes all the permutations and saves them in Answer: */
?- findall(Perm, permutations([0,1,2,...,size], Perm), Answer).
===================================================
One way of sorting a deck of cards is by computing all the shuffles (permutations) and keeping the one that places the cards in order. But this strategy will be very slow! How slow?
Permutation problems, like all-N-shuffles and travelling-salesman-to-N-cities,
require 1*2*3*..upto..*N data-structure lookups/updates to compute their answers.
This number is abbreviated as N!, called factorial N, and it grows huge quickly:
N log2N N2 N*log2N N!
-------------------------------------------------------
64 6 4096 384 126886932185884164103433389335161480802865516174545192198801894375214704230400000000000000
512 8 262,144 4096 347728979313260536328304591754560471199225065564351457034247483155161041206635254347320985033950225364432243311021394545295001702070069013264153113260937941358711864044716186861040899557497361427588282356254968425012480396855239725120562512065555822121708786443620799246550959187232026838081415178588172535280020786313470076859739980965720873849904291373826841584712798618430387338042329771801724767691095019545758986942732515033551529595009876999279553931070378592917099002397061907147143424113252117585950817850896618433994140232823316432187410356341262386332496954319973130407342567282027398579382543048456876800862349928140411905431276197435674603281842530744177527365885721629512253872386613118821540847897493107398381956081763695236422795880296204301770808809477147632428639299038833046264585834888158847387737841843413664892833586209196366979775748895821826924040057845140287522238675082137570315954526727437094904914796782641000740777897919134093393530422760955140211387173650047358347353379234387609261306673773281412893026941927424000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
10,000 12 100,000,000 120,000 ????????????????????????????????????????????????????????????????????????????????
===================================================
No computer, no matter how fast, can use a
factorial-time algorithm to solve a problem of realistic size. A problem that has no faster solution than this is
called intractable --- unsolvable in practice.
There is a way to improve the performance of permutation problems:
remember partial solutions and reuse them.
You can do this in the travelling-salesman problem, where the distances
over subpaths in the graph can be saved in a table and reused as needed
when computing longer paths. (This technique is called
dynamic programming.) The resulting algorithm uses about
2N lookups --- exponential time:
N log2N N2 N*log2N 2N
-------------------------------------------------------
64 6 4096 384 18446744073709551616
512 8 262,144 4096 13407807929942597099574024998205846127479365820592393377723561443721764030073546976801874298166903427690031858186486050853753882811946569946433649006084096
10,000 12 100,000,000 120,000 ????????????????????????????????????????????????????????????????????????????????
Exponential-time algorithms are still too slow to use in practice.
At best, you start one and come back in a day or two. (I am not kidding; people do this.) For this reason, a problem with at best an expoential-time solution is
still considered intractible.
Computational complexity theory is the study of the fundamental time and space requirements for solving important problems.
In the 19th century, mathematicians started working with sets, defining
them in terms of membership properties, like this:
===================================================
Pos = { n | n > 0 }
W3 = { s | s is a string of length 3 }
EvenPos = { n | n > 0 and n / 2 has remainder 0 }
===================================================
You can ask if a value, v, is a member of a set, S, like this: v ∈ S, e.g.,
3 ∈ Pos holds True
"xyz" ∈ Pos holds False, which means not("xyz" ∈ Pos) holds True
"xyz" ∈ W3 holds True
You can use ∈ in the membership property, too:
===================================================
EvenPos = { n | n ∈ Pos and n / 2 has remainder 0 }
===================================================
A computer person thinks of a set as a kind of "function" that is
"called" when you ask it a membership question, e.g.,
3 ∈ Pos is like calling Pos(3) and expecting back an answer
of True or False.
Sets can hold other sets, which makes the concept really interesting.
Consider this example:
===================================================
NE = { S | not(S = {}) }
===================================================
NE collects those values --- including sets --- that aren't the empty set.
For example,
Pos ∈ NE
2 ∈ NE
but {} ∈ NE holds False
Now, is it that
NE ∈ NE ?
Well, yes, because NE is a nonempty set. So, NE contains itself as well.
The membership question just stated is an example of
self-reflection.
All sets can do self-reflection, e.g.,
not(Pos ∈ Pos) holds True and is a reasonable answer to the question.
Bertrand Russell observed that this convenient way of defining sets via membership properties was flawed in the sense that some sets cannot be defined. Here is Russell's paradox:
The collection clearly has members --- those sets that do not hold themselves as members, e.g., {} ∈ R holds True but not(NE ∈ R), since NE ∈ NE holds True.
R ∈ RExplain why a True answer is impossible. Explain why a False answer is impossible. Therefore, R cannot be defined as a set, despite the fact we used the standard, accepted membership-property language.
V | |1|0|1|1| |and it moves to the right of the int, till it finds the rightmost digit:
V
| |1|0|1|1| |
Then it adds one and does the needed carries until it is finished:
V
| |1|1|0|0| |
Finally, it resets to its start position:
V | |1|1|0|0| |Although you might find this exercise tedious, it is solved at the same level of detail as programs written in assembly language for operating-system kernels and device drivers.
Finish this exercise as follows:
How far did you progress with your experiments until your computer failed to respond? Is the computer lost? tired? worn out? What if you bought a new computer that is twice as fast or even ten times as fast as the one you are now using --- would it help here? Is it realistic to compute all the permutations of an ordinary 52-card deck of cards so that you can prepare for your next trip to Las Vegas? Can't computers do things like this?
def isOrdered(nums) :
"""isOrdered looks at the int list, nums, and returns True if
nums is ordered. It returns False if nums is not ordered."""
Use your function with this one:
def sortList(nums) :
"""sortList finds the sorted permutation of int list nums by brute force"""
allindexpermutations = permutations(len(nums))
for indexperm in allindexpermutations :
possibleanswer = []
for i in indexperm :
possibleanswer = possibleanswer.append(nums[i-1])
print "Possible sorted version is", possibleanswer
if isOrdered(possibleanswer) :
print "Found it!"
return possibleanswer
Find a better way of sorting a list of ints.
Here are two solutions for sorting in Prolog.
Run them:
/**** NAIVE SPECIFICATION OF A SORTED LIST ****/
/* sorted(Xs, Ys) holds when Ys is the sorted variant of Xs */
sorted(Xs, Ys) :- permutation(Xs, Ys), ordered(Ys).
/* permutation(Xs, Zs) holds true if Zs is a reordering of Xs */
permutation([], []).
permutation(Xs, [Z|Zs]) :- select(Z, Xs, Ys), permutation(Ys, Zs).
/* select(X, HasAnX, HasOneLessX) "extracts" X from HasAnX,
giving HasOneLessX */
select(X, [X|Rest], Rest).
select(X, [Y|Ys], [Y|Zs]) :- select(X, Ys, Zs).
/* ordered(Xs) is true if the elements in Xs are ordered by <= */
ordered([]).
ordered([X]).
ordered([X,Y|Rest]) :- X =< Y, ordered([Y|Rest]).
/*** INSERTION SORT: an efficient search for an ordered list ***/
/* isort(Xs, Ys) generates Ys so that it is the sorted
permutation of Xs */
isort([], []).
isort([X|Xs], Ys) :- isort(Xs, Zs), insert(X, Zs, Ys).
/* insert(X, L, LwithX) inserts element X into list L,
generating LwithX */
insert(X, [], [X]).
insert(X, [Y|Ys], [X, Y | Ys]) :- X =< Y.
insert(X, [Y|Ys], [Y|Zs]) :- X > Y, insert(X, Ys, Zs).
Start with these codings of the sets listed earlier:
def pos(n) :
return isinstance(n, int) and n > 0
def W3(s) :
return isinstance(s, string) and len(s) == 3
def emptyset(v) : return False
def R(S) :
import collections
return isinstance(S, collections.Callable) and not(S(S))
Try these: pos(2); pos("abc"); W3("abc"); W3(pos); pos(pos); emptyset(2); emptyset(W3).
Now try these: R(2); R(pos); R(emptyset); R(R).
Here is an attempt to define the set of non-empty sets, NE. What isn't quite correct here?
(This is a really a question about how Python checks ==.)
def NE(S) : return S == emptyset
Is it possible to repair this code so that it works correctly in Python? Why not?
David Schmidt das at ksu.edu
This work is licensed under a Creative Commons License.
|